Adaptive Mesh RefinementFlexPDE continually monitors the accuracy of the solution, and adapts the finite element mesh to resolve those areas of high error.
You don't need a dense mesh throughout the domain, because FlexPDE will find the areas that need it, and put it there!
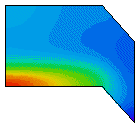
The problem shown here is a two-phase flow calculation, modeling the extraction of oil by water injection. FlexPDE adapts the mesh to the front of the wave.
Arbitrary Lagrange/Eulerian moving mesh*FlexPDE 6 allows the definition of mesh-moving equations*, and applies an Arbitrary Lagrange/Eulerian (ALE) formulation. This allows several optional behaviors:
- By locking the mesh to the fluid velocity, you can create a fully Lagrangian model.
- Or, you can define a relaxive mesh within moving boundaries to maintain mesh integrity.
- Or, by omitting the mesh moving equations, you can perform a fully Eulerian computation.
In any case, FlexPDE automatically corrects the PDE system to represent the motion of the mesh.
The problem shown here computes the motion of a gas in a compressor cylinder.
|
Animate |
|||
(All animations are FlexPDE native graphical output, assembled into a movie by AnimationShop)
*Note: FlexPDE 6 does not support slip surfaces.
Gas Pressure
Use Table at left
to animate display
